by Jean-Charles TASSAN & Brent R. Antonson
What you’re looking at in this gallery is an attempt to do two things at once: explain a tiny mechanical heartbeat of quantum interaction, and make that heartbeat visible. The theoretical line is Jean-Charles’s: a compact formalism that describes how electrons exchange energy via photons. The visual line is mine — kinetic maps that translate that formalism into moving images.
If that sounds dense, cool. That’s why we made pictures. Here’s the essay version — stripped down, practical, and honest.
The one-sentence scaffold
RES = RAG / T_real. Read it as: resonance (RES) is the result of a resonant amplitude gradient (RAG) distributed across a finite, measurable transfer interval (T_real).
That’s not a mystical slogan. It’s bookkeeping: when energy moves between particles, two things matter most — how well the oscillations line up (resonance) and how long the in-between interval lasts (T_real). RAG is the way resonant strength spreads through the field. Divide the spread by time and you get the instantaneous measure of coherence: RES.
The actors: k_res and k_struct
Two handily minimalist knobs drive everything we show:
- k_res — the resonance coefficient (0 → 1). At k_res = 1 the emitter and absorber are phase-locked; coherence is perfect. At values below 1, the match is partial and the system is structurally richer (more nodes, more interference).
- k_struct — the structural index (> 1 when complexity rises). Higher k_struct means more branching, more transient form, more interference patterns to resolve.
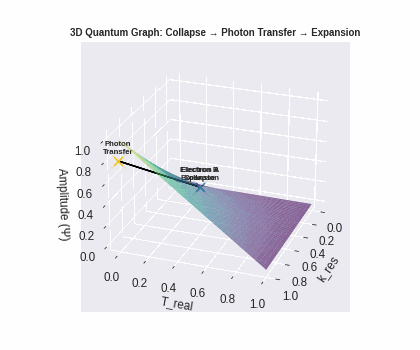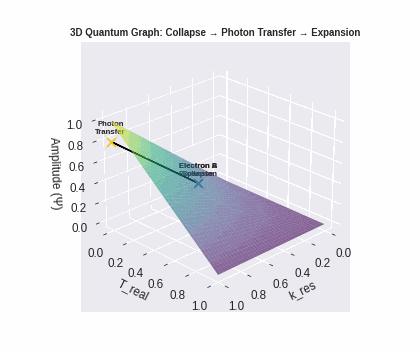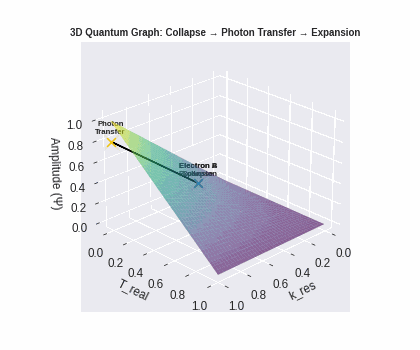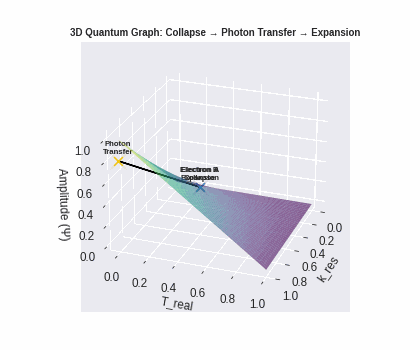
These knobs let us speak of physical events in three simple frames: Collapse, Transfer, and Expansion.
Collapse — emission, concentrated coherence
Parameter setting: k_res = 1 → k_struct = 1
Imagine a charged electron in an excited orbital. At emission, its orbital contracts and phase-locks with the emitted photon. That contraction is the collapse: energy condenses into a coherent wavepacket that leaves the emitter as a continuous, highly ordered signal. Structure simplifies — there are few degrees of freedom. Visually, the loop tightens into a luminous spine.
Why call this “collapse”? Because a previously broad distribution of phase possibilities resolves into a single, high-fidelity emission. In information terms, entropy locally drops as the system selects a phase-coherent channel.
Transfer — the photon crosses T_real
Parameter setting: 0 < k_res < 1 → k_struct > 1
Once the photon departs, the field is no longer a single, neatly ordered spine. The traveling photon carries phase, amplitude and energy across space; in so doing, it couples to other degrees of freedom in the field. Resonance weakens. Structural complexity spikes: interference fringes, transient nodes, branching — the system looks messier because it’s open to interactions.
This is where T_real becomes central. T_real is the finite, physically measurable interval between emission and absorption. It’s not a convenient zero; it’s a domain where decoherence, scattering, and field-mediated structure happen. In our notation, RAG quantifies how the resonant amplitude fans out across the field during T_real. The ratio RAG/T_real gives you the instantaneous resonance metric — RES — that determines how coherently the signal will be received.
Expansion — absorption, resonance regained
Parameter setting: k_res = 1 → k_struct = 1
The photon’s arrival at the receiving orbital re-establishes phase locking. The receiving electron’s orbital expands as it absorbs the photon. Structure simplifies again; coherence returns. In practical terms, the transfer is almost instantaneous at the endpoints — an implosion (emitter) coupled to an explosion (receiver) — but bound across space by the finite crossing time of T_real.
Why this framing matters
This trio — collapse, transfer, expansion — is a minimal lifecycle of coherent energy exchange. It gives you a way to reason about:
- Coherence management: what lets a signal survive transit across a noisy field? Short, high-RES transfers.
- Information fidelity: how much of the original phase and amplitude survives? That depends on RAG and T_real.
- Transient structure: where and why interference and branching appear — exactly in the transfer frame where k_res < 1 and k_struct > 1.
In short: the clean moments are at the endpoints; the messy, informative moments happen in between.
A note on physics vs. metaphor
We’re not claiming a cure for quantum mysteries. Jean-Charles’s equations (linked in the full paper) formalize these notions; the gallery translates them. Think of the essay as an operational map: this is how the math looks when you animate it. For physicists, it’s a suggestive architecture; for artists, it’s a formal grammar for depicting how interactions feel; for curious readers, it’s a taxonomy of “how coherence behaves.”
Visual cues (how to read the loops)
- Loop I – Collapse: tight, luminous spine; few nodes; accelerated phase movement. (Emission)
- Loop II – Transfer: filamentary photon path; branching nodes; temporary interference structures. (Transit)
- Loop III – Expansion: receiving orbital expands into coherent glow; resolution returns. (Absorption)
Why you should care
This is a minimal model for how information moves in the quantum field. It’s useful for thinking about quantum communication, decoherence control, and even metaphors of distributed computation. More practically: it helps designers and scientists think in units of coherence (RES) rather than just energy or frequency.