Abstract
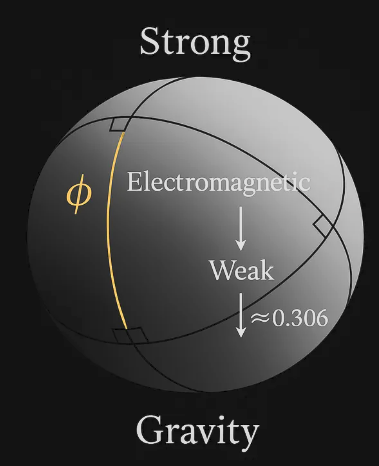
We propose that the four known fundamental interactions — strong, weak, electromagnetic, and gravitational — may have emerged from a primordial φ-structured manifold. By embedding dimensionless constants such as the golden ratio (φ ≈ 1.618) and the ecliptics principle constant (≈ 0.306) into a spherical geometry of eight tri-rectangles (spherical triangles with three 90° angles), we suggest a mechanism where force unification fractures through critical ratios. This approach seeks to identify the “fractal constants” of symmetry breaking, with implications for quantum gravity and unified field theory.

1. Introduction

  • The unification problem: four forces, one origin.
  • Standard approaches: GUTs (SU(5), SO(10), E₈) rely on group symmetry, but lack a natural, dimensionless fracture constant.
  • Our question: Could φ and related ratios govern the symmetry breaking thresholds?

2. Geometric Prelude: Tri-Rectangles and the Spherical Octant

  • Define the “tri-rectangle” as a spherical triangle with three right angles.
  • Eight tri-rectangles tile a sphere (octant structure).
  • This geometry mirrors SU(2)/SO(3) rotational symmetries.
  • Proposal: the manifold of the early universe could be modeled as a φ-scaled hypersphere tessellated in this way.

3. Dimensionless Attractors: φ and the Ecliptics Constant

  • φ (1.618…): appears in recursive bifurcations, Penrose tilings, eigenvalue scaling.
  • Ecliptics constant (~0.306): a potential secondary attractor, governing phase alignment and critical bifurcations.
  • Hypothesis: These constants act as fracture parameters that determine how symmetries split.

4. Force Fracturing as Critical Ratios

  • Stage 1: Unified Force → splits at φ into (Strong + Electroweak).
  • Stage 2: Electroweak → splits at 0.306 into (Electromagnetic + Weak).
  • Stage 3: Gravity remains as manifold curvature, not a split, but the “container” of the process.
  • Analogy to Feigenbaum constants in chaos: universal numbers governing bifurcation thresholds.

5. Mathematical Sketch

  • Let F = Fracture Constant.
  • Assume an initial manifold symmetry G (e.g., SO(10) or E₈).
  • Define fracturing process as:G → φ-split → G1 ⊗ G2
    G2 → 0.306-split → G3 ⊗ G4
  • Eigenvalue conjecture: Laplace–Beltrami spectra on φ-structured octants yield scaling constants near φ and 0.306.

6. Why Only Four Forces?

  • If no further critical constants exist below Planck scale, the system stabilizes at four.
  • Suggests that “fourness” is emergent from geometry + ratios, not arbitrary.

7. Implications for Quantum Gravity

  • Gravity reframed: not a gauge force, but the φ-structured curvature of the manifold itself.
  • Unification occurs not by adding gravity in, but by recognizing its geometric root.
  • This could allow a dimensionless entry point for quantum gravity.

8. Path Forward

  • Test coupling constant unification at Planck scale against φ-scaling.
  • Compute spherical Laplacian eigenvalues on φ-octants.
  • Explore links with Feigenbaum universality and recursive criticality.

9. Conclusion

If φ and its companions serve as fracture constants for the forces, then physics may not just be written in the language of symmetry, but in the grammar of proportion. The four forces would then be not arbitrary remnants of cooling, but the necessary harmonics of a universe tuned by φ.

Share this post